Mixed-precision training in LLM

a note on mixed-precision training

Background

Float Precision in Deep Learning

In the realm of deep learning, using 64-bit floating point operations is considered unnecessary and computationally expensive since 64-bit operations are generally more costly, and GPU hardware is also not optimized for 64-bit precision. So instead, 32-bit floating point operations (also known as single-precision) have become the standard for training deep neural networks on GPUs. In fact, PyTorch uses 32-bit floats by default.

Technical Background on Floating-point Representation

In the context of floating-point numbers, “bits” refer to the binary digits used to represent a number in a computer’s memory. In floating-point representation, numbers are stored in a combination of three parts: the sign, the exponent (the power number of 2), and the significand (faction value).

There are three popular floating point formats

Float32 (FP32): sign 1 bit, exponent 8 bit and fraction 23 bit, 4 bytes.
Float16 (FP16): sign 1 bit, exponent 5 bit and fraction 10 bit, 2 bytes.
BFloat16 (Brain Floating Point, BF16): sign 1, exponent 8 and fraction 7 bit, 2 bytes.

floating-point formats	total bits	exp bit	fraction bit	range in numbers	decimal precision
FP32	32	8	23	±10e^38	10-6
FP16	16	5	10	±10e^4	10-3
BF16	16	8	7	±10e^38	10-2
INT16	16	15	0	±10e^4	1
INT8	8	7	0	±10e^2	1
INT4	4	3	0	±10e^1	1

For instance, if the Qwen2-72b model is stored in bf-16 format, it would require approximately $72706203648 \times 16$ bits of memory, which translates to about $1163299258368$ bits, or roughly 135.4 GB.

FP32 vs FP16

fp16 uses three fewer bits for the exponent and 13 fewer bits for the fractional value: it represent a narrower range of numbers with less precisions.

FP32 vs FP16 vs BF16

fp32 and fp16 represent the same range of values as their exponents both have 8 bits. Compared to fp32 and fp16, bf32 has lowest precision. But in most applications, this reduced precision has minimal impact on modeling performance.

The code below reveals that the largest float32 number is 3.40282e+38; float16 numbers cannot exceed the value 65,504.

import torch

torch.finfo(torch.float16)
> finfo(resolution=0.001, min=-65504, max=65504, eps=0.000976562, smallest_normal=6.10352e-05, tiny=6.10352e-05, dtype=float16)

torch.finfo(torch.float32)
> finfo(resolution=1e-06, min=-3.40282e+38, max=3.40282e+38, eps=1.19209e-07, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=float32)

# torch.cuda.is_bf16_supported() # check if bfloat16 is suppored in cuda
torch.finfo(torch.bfloat16)
> finfo(resolution=0.01, min=-3.38953e+38, max=3.38953e+38, eps=0.0078125, smallest_normal=1.17549e-38, tiny=1.17549e-38, dtype=bfloat16)

Mixed-Precision Training

Instead of running all parameters and operations on FP16, we switch between FP32 and FP16 operations during training, hence, the term “mixed” precision.

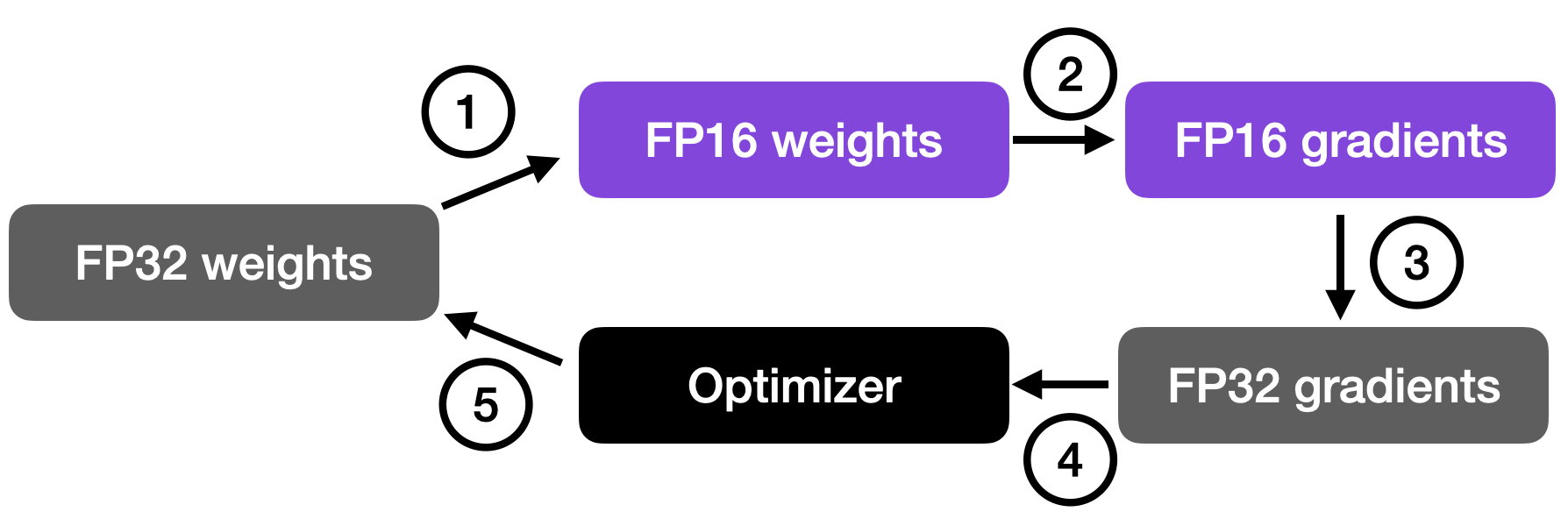
Image Source: Mixed-Precision Training Mechanics

The training process typically involves four steps:

step 1: convert FP32 weights to FP16 weights of neworks, for faster computation.
step 2: compute gradient using FP16 precision.
step 3: convert FP16 gradient to FP32 gradient to maintain numerical stability.
step 4: multiplied by learning rate and update weight in FP32 precision.

To summarize:

parameters and activations are stored as FP16, enabling the use of the high throughput tensor core units on these GPUs. During mixed-precision training, both the forward and backward propagation are performed using fp16 weights and activations.
To effectively compute and apply the updates at the end of the backward propagation, the mixed-precision optimizer keeps an FP32 copy of the parameters as well as an FP32 copy of all the other optimizer states. Now the mixed precision method now has been the state-of-the-art approach to train LLMs on the current generation of NVIDIA GPUs.

Memery Consumption Estimation in Mixed-Precision Training

During model training, most of the memory is consumed by model states, i.e., tensors comprising of optimizer states, gradients, and parameters. Besides these model states, the rest of the memory is consumed by activations, temporary buffers and fragmented memory which is called residual states.

Memory Consumption Estimation of Model States

Assume we are training a model with $N$ parameters using the Adam optimizer. This requires:

FP16 copies of the parameters and gradients: Both the parameters and gradients are stored in FP16 format, each requiring $ 2N$ bytes of memory$N * 16 bit / 8 bit per byte = 2N$., for a total of $4N$ bytes.
Optimizer states: Adam requires FP32 copies of the parameters, momentum, and variance. The memory requirements for these are $4N$ bytes each, resulting in a total of $12N$ bytes.

Thus, the total memory in bytes required for training the model is: $ 2N + 2N + 3 \times 4N = 16N $

During inference, only the model parameters are stored, consuming $2N$ bytes of memory (since only the FP16 parameters are needed).

For example, to train a model like Mistral-7B-FP16 with 7 billion parameters ($ N = 7 \times 10^9 $ bit), the memory requirement would be at leastWe simply assume $N * 1,000 * 1,000 * 1,000 / 1024 / 1024 / 1024 \approx 1$.: $ 7 \times 10^9 \times 16 / (1024^3(bytes per GB)) \approx 112 GB. $

For inference, the memory requirement is lower, using only: $ 7 \times 10^9 \times 2 / (1024^3(bytes per GB)) \approx 14 GB. $